The physical layer is the interface to the analog fading world and the parameters to be determined are often subject to very short-term changes, especially for mobile users. Therefore, an improvement of the parameter estimation by a longer learning time is not possible. Hence, the flow of additional information or the application of suitable models must then be used to an advantage.
One application is the determination of the current traffic density, which can be very dynamic. For this purpose, solution approaches that integrate additional information [1], [2], [3] have been developed and researched. However, faster converging algorithms can also be used successfully [4].
Another important topic is the generation of a quasi-reciprocity for frequency duplex systems (FDD-systems) in order to successfully apply massive MIMO and time reversal algorithms with these systems. The department of Wireless Communications and Networks pursues different research approaches in this area [5], [6], [7], [8].
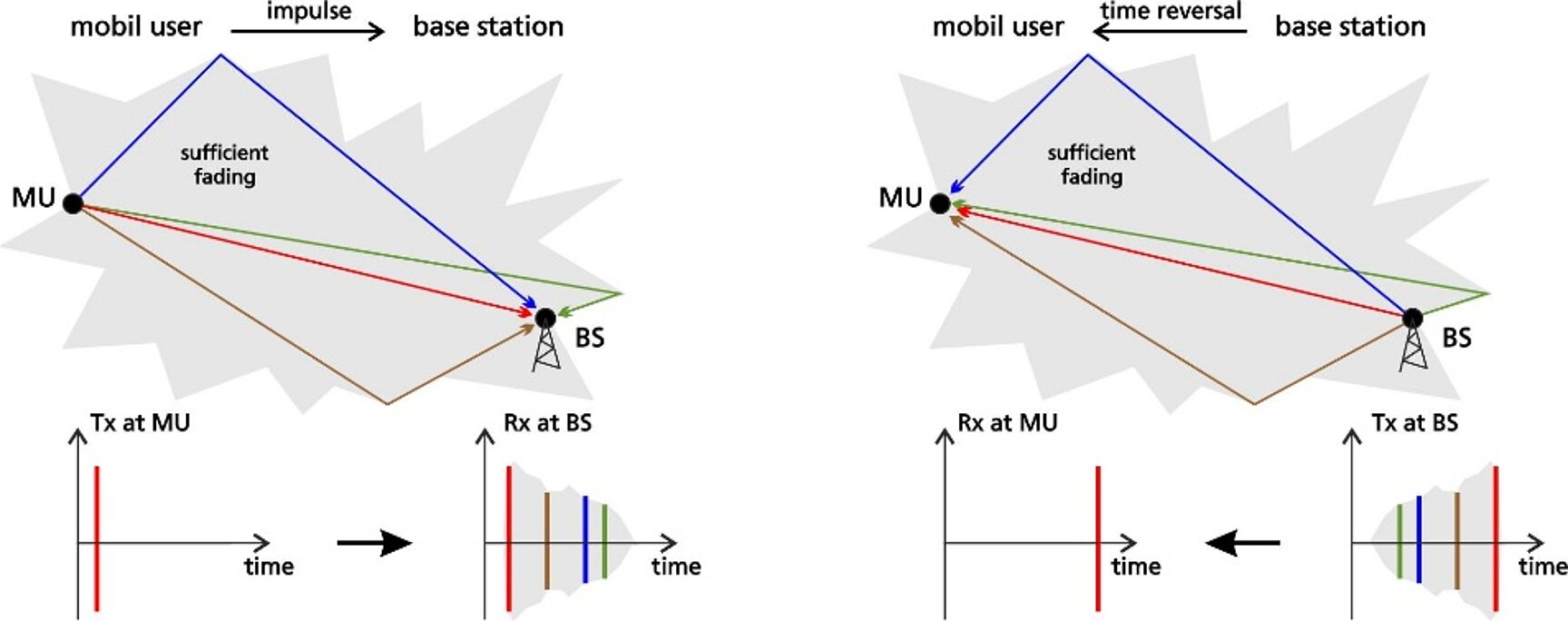
The current research topic of time reversal (see figure) must also be established in the physical layer, because the fading properties must be clearly determined within the coherence time of the channel. This is the only way to use the receive pattern successfully to define the next transmission pattern.
Further research work of the department of Wireless Communication and Networks on the application of Machine Learning in the physical layer deals with, among other things: Cell-less systems [9], nonlinear beamforming [10], peak-to-average power ratio (PAPR) reduction [11], [12] and massive random access [13].
References
[1] D. A. Awan, R. L. G. Cavalcante, and S. Stańczak, "A robust machine learning method for cell-load approximation in wireless networks," in Proc. IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Apr. 2018
[2] R. L. G. Cavalcante, Y. Shen, S. Stańczak, "Elementary Properties of Positive Concave Mappings with Applications to Network Planning and Optimization," IEEE Trans. Signal Processing, vol. 64, no. 7, pp. 1774-1783, April 2016
[3] R. L. G. Cavalcante, M. Kasparick, and S. Stańczak, "Max-min utility optimization in load coupled interference networks," IEEE Trans. Wireless Comm., vol. 16, no. 2, pp. 705-716, Feb. 2017
[4] D. A. Awan, R. L. G. Cavalcante, M. Yukawa, and S. Stańczak, "Detection for 5G-NOMA: An Online Adaptive Machine Learning Approach," in Proc. IEEE International Conference on Communications (ICC), May 2018
[5] R. L. G. Cavalcante, L. Miretti, and S. Stańczak, "Error bounds for FDD massive MIMO channel covariance conversion with set-theoretic methods," in Proc. IEEE Global Telecommunications Conference (GLOBECOM), Dec. 2018
[6] A. Decurninge, M. Guillaud, and D.T.M. Slock, “Channel covariance estimation in massive MIMO frequency division duplex systems,” in IEEE Globecom, 2015
[7] L. Miretti, R. L. G. Cavalcante, and S. Stańczak, "Downlink channel spatial covariance estimation in realistic FDD massive MIMO systems," IEEE Global Conference on Signal and Information Processing (GlobalSIP), 2018
[8] L. Miretti, R.L.G. Cavalcante and S. Stanczak, „FDD Massive Channel Spatial Covariance Using Projection Methods, in Proc. IEEE ICASSP, April 2018
[9] D. A. Awan, R. L. G. Cavalcante, Z. Utkovski, and S. Stanczak, “A set-theoretic method for detection in cell-less systems,” submitted
[11] J. Fink, R. L. G. Cavalcante, and S. Stańczak, “Extrapolated Projection Methods for PAPR reduction," submitted
[12] R. L. G. Cavalcante and I. Yamada, "A flexible peak-to-average power ratio reduction scheme for OFDM systems by the adaptive projected subgradient method,” IEEE Trans. Signal Processing, vol. 57, no. 4, pp. 1456-1468, April 2009
[13] P. Agostini, Z. Utkovski, J. Pilz, S. Stanczak, Scalable massive random access in C-RAN with fronthaul limitations, submitted