The concept of rate-distortion optimized encoding is applicable to all video coding standards. It significantly improves coding efficiency in comparison to encoding techniques that do not include this concept.
Video coding standards are designed for enabling interoperability between products of different vendors. It has to be ensured that the video signal encoded by each vendor's product can be reliably decoders by others. For that reason, only the bitstream syntax and the decoding process are standardized. Other components of a video transmission such as pre-processing, encoding, loss/error recovery, and post-processing are intentionally left out of scope.
Besides enabling interoperability, the primary goal of video coding standards development is to optimize coding efficiency, i.e., the ability to minimize the bit rate necessary for representing a given level of video quality (or the maximize the video quality for a given maximum bit rate). The end-to-end coding efficiency, however, is mainly determined at the encoder side. Since video coding standards do not specify the encoding process, they do not guarantee any particular coding efficiency. The encoder control, which determines the syntax elements of a video bitstream given an input video sequences, is the crucial part for optimizing the coding efficiency.
The Image and Video Coding Group was very active in optimizing the encoder control for different video coding standards. The investigated encoder control concepts have become an integral part of the reference model and reference software for the video coding standards H.264/AVC and HEVC. The techniques are also used during the standardization process in order to evaluate the potential coding efficiency improvement that a tool proposed for inclusion in the standard provides.
Lagrange Optimization in Image and Video Encoding
The task of an encoder control for a particular coding standard is to determine the values of the syntax elements, and thus the bitstream b, for a given input sequence s in a way that the distortion D(s,s') between the input sequence s and its reconstruction s=s'(b) is minimized subject to a set of constraints, which usually includes constraints for the average and maximum bit rate and the maximum coding delay. Let Bc be the set of all conforming bitstreams that obey the given set of constraints. For any particular distortion measure D(s,s'), the optimal bitstream in rate-distortion sense is given by
| b* = | arg min b ∈ Bc | D(s,s′(b)) |
Due to the huge parameter space and encoding delay, it is impossible to directly apply this minimization. Instead, the overall minimization problem is split into a series of smaller minimization problems by partly neglecting spatial and temporal interdependencies between coding decisions.
Let sk be a set of source samples, such as a video picture or a block of a video picture, and let p ∈ Pk be a vector of coding decisions (or syntax element values) out of a set Pk of coding options for the set of source samples sk. The problem of finding the coding decisions p that minimize a distortion measure Dk(p)=D(sk,s'k) between the original samples sk and their reconstructions s'k=s'k(p) subject to a rate constraint Rc can be formulated as
| min p ∈ Pk | Dk(p) | subject to | Rk(p ≤ RC), |
where Rk(p) represents the number of bits that are required for signaling the coding decisions p in the bitstream. Other constraints, such as the maximum coding delay or the minimum interval between random access points, shall be considered by selecting appropriate prediction structures and coding options. This constrained minimization problem can be reformulated as an unconstrained minimization,
| min p ∈ Pk | Dk(p) + λ ⋅ Rk(p), |
where λ ≥ 0 denotes the so-called Lagrange multiplier.
If a set of source samples sk can be partitioned into a number of subsets sk,i in a way that the associated coding decisions pi are independent of each other and an additive distortion measure Dk,i(pi ) is used, the minimization problem can be written as
| ∑ i | min pi ∈ Pk,i | Dk,i(pi) + λ ⋅ Rk,i(pi). |
The optimal solution of this optimization problem can be obtained by independently selecting the coding options pi for the subsets sk,i. Although most coding decisions in a video encoder cannot be modeled as independent, for a practical applicability of the Lagrangian encoder control, it is required to split the overall optimization problem into a set of feasible decisions. While past decisions are taken into account by determining the distortion and rate terms based on already coded samples, the impact of a decision on future samples and coding decisions is ignored. The used distortion measures D are defined as
| ∑ i ∈ B | |si - s′i|p, |
with p = 1 for the sum of absolute differences (SAD) and p = 2 for the sum of squared differences (SSD). si and s'k represent the original and reconstructed samples, respectively, of a considered block B.
Application of Lagrange Optimization in Video Encoding
The approach of Lagrange optimization has been applied to different aspects of the video encoder control:
- Determination of motion vectors for motion-compensated macroblocks
- Determination of reference indices for multi-frame motion-compensated prediction
- Determination of intra prediction modes
- Determination of macroblock and sub-macroblock coding modes
- Determination of transform coefficient levels
The r-d optimized encoder control has been applied for the following video coding standards:
- H.262/MPEG-2 Video
- H.263
- MPEG-4 Visual
- H.264/MPEG-4 AVC
- HEVC
For H.263, the encoder control design led to the creation of a new test model TMN-10. For H.264/AVC, some aspects of the Lagrangian encoder control were already included in the first Test Model, the complete Lagrangian encoder control has been included during the development process. The Lagragian encoder control was used from the beginning for the development of the SVC and MVC extension of H.264/AVC and for the HEVC development. Furthermore, the rate-distortion optimized encoder control has been used as basis for:
- Optimizing encoders for error-prone environments [4]
- Developing a multi-layer encoder for SVC
- Developing an optimized encoder for lapped transforms [5]
Efficiency of the Lagrangian coder control
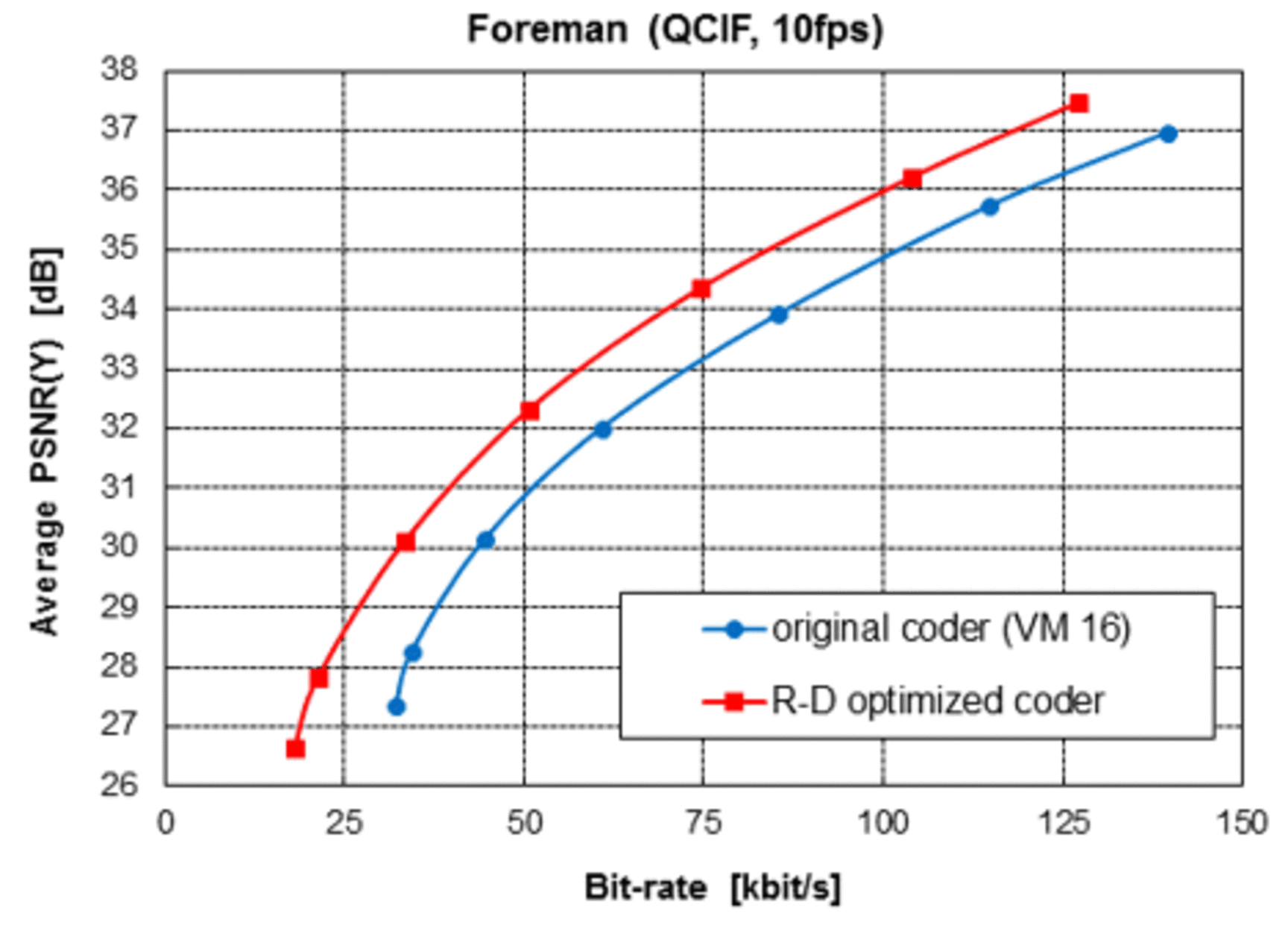
The efficiency of the Lagrangian encoder control is demonstrated on an example for MPEG-4 Visual. Figure 1 compares the coding efficiency that is achieved with the Lagrangian encoder control with the coding efficiency obtained by using the Verification Model 16 (Test Model developed by MPEG), which does not include Lagrangian optimization.
References
- G. J. Sullivan and T. Wiegand, "Rate-Distortion Optimization for Video Compression," IEEE Signal Processing Magazine, Nov. 1998.
- T. Wiegand, H. Schwarz, A. Joch, F. Kossentini, G. J. Sullivan, "Rate-constrained coder control and comparison of video coding standards," IEEE Trans. on Circuits and Systems for Video Technology, July 2003.
- J.-R. Ohm, G. J. Sullivan, H. Schwarz, T. K. Tan, T. Wiegand, "Comparison of the Coding Efficiency of Video Coding Standards," IEEE Trans. on Circuits and Systems for Video Technology, to appear.
- T. Stockhammer, D. Kontopodis, and T. Wiegand, "Rate-distortion optimization for JVT/H.26L Video Coding in Packet Loss Environments," Packet Video Workshop, April 2002.
- M. Winken, D. Marpe, and T. Wiegand, "Global and local rate-distortion optimization for Lapped Biorthogonal Transform Coding," IEEE Intl. Conf. on Image Processing, Sept. 2010.